Nội dung chính
Sắp xếp chọn (Selection Sort) là gì?
Sắp xếp chọn (Selection Sort) là một giải thuật đơn giản. Giải thuật sắp xếp này là một giải thuật dựa trên việc so sánh in-place, trong đó danh sách được chia thành hai phần, phần được sắp xếp (sorted list) ở bên trái và phần chưa được sắp xếp (unsorted list) ở bên phải. Ban đầu, phần được sắp xếp là trống và phần chưa được sắp xếp là toàn bộ danh sách ban đầu.
Phần tử nhỏ nhất được lựa chọn từ mảng chưa được sắp xếp và được tráo đổi với phần bên trái nhất và phần tử đó trở thành phần tử của mảng được sắp xếp. Tiến trình này tiếp tục cho tới khi toàn bộ từng phần tử trong mảng chưa được sắp xếp đều được di chuyển sang mảng đã được sắp xếp.
Giải thuật này không phù hợp với tập dữ liệu lớn khi mà độ phức tạp trường hợp xấu nhất và trường hợp trung bình là O(n2) với n là số phần tử.
Cách giải thuật sắp xếp chọn (Selection Sort) làm việc
Dưới đây là các hình minh họa cho cách giải thuật sắp xếp chọn làm việc. Giả sử chúng ta có một mảng như sau:

Từ vị trí đầu tiên trong danh sách đã được sắp xếp, toàn bộ danh sách được duyệt một cách liên tục. Vị trí đầu tiên có giá trị 14, chúng ta tìm toàn bộ danh sách và thấy rằng 10 là giá trị nhỏ nhất.

Do đó, chúng ta thay thế 14 với 10. Sau một vòng lặp, giá trị 10 thay thế cho giá trị 14 tại vị trí đầu tiên trong danh sách đã được sắp xếp. Chúng ta tráo đổi hai giá trị này.

Tại vị trí thứ hai, giá trị 33, chúng ta tiếp tục quét phần còn lại của danh sách theo thứ tự từng phần tử.

Chúng ta thấy rằng 14 là giá trị nhỏ nhất thứ hai trong danh sách và nó nên xuất hiện ở vị trí thứ hai. Chúng ta tráo đổi hai giá trị này.

Sau hai vòng lặp, hai giá trị nhỏ nhất đã được đặt tại phần đầu của danh sách đã được sắp xếp.

Tiến trình tương tự sẽ được áp dụng cho phần còn lại của danh sách. Các hình dưới minh họa cho các tiến trình này.
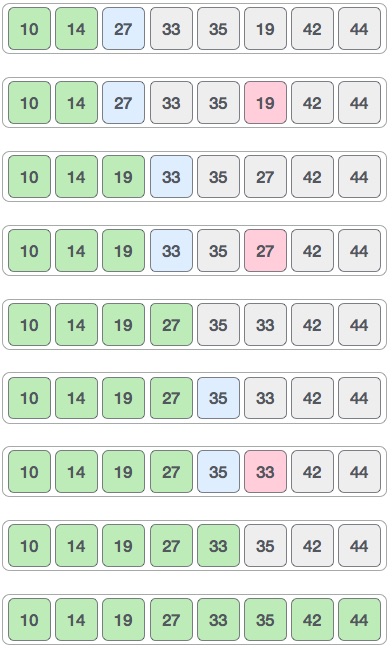
Tiếp theo chúng ta sẽ theo dõi một số khía cạnh khác của giải thuật sắp xếp chọn.
Giải thuật cho sắp xếp chọn (Selection Sort)
Bước 1: Thiết lập MIN về vị trí 0 Bước 2: Tìm kiếm phần tử nhỏ nhất trong danh sách Bước 3: Tráo đổi với giá trị tại vị trí MIN Bước 4: Tăng MIN để trỏ tới phần tử tiếp theo Bước 5: Lặp lại cho tới khi toàn bộ danh sách đã được sắp xếp
Giải thuật mẫu cho sắp xếp chọn
Bắt đầu giải thuật sắp xếp chọn (Selection Sort)
list : mảng các phần tử
n : kích cỡ mảng
for i = 1 tới n - 1
/* thiết lập phần tử hiện tại là min*/
min = i
/* kiểm tra phần tử có là nhỏ nhất không */
for j = i+1 tới n
if list[j] < list[min] thì
min = j;
kết thúc if
kết thúc for
/* tráo đổi phần tử nhỏ nhất với phần tử hiện tại*/
if indexMin != i then
tráo đổi list[min] và list[i]
kết thúc if kết thúc for
Kết thúc giải thuật

