Bài tập C++ - Tìm ước số chung lớn nhất (USCLN) và bội số chung nhỏ nhất (BSCNN) của 2 số

Đề bài

Viết chương trình C++ tìm ước số chung lớn nhất (USCLN) và bội số chung nhỏ nhất (BSCNN) của hai số nguyên dương a và b.

Định nghĩa

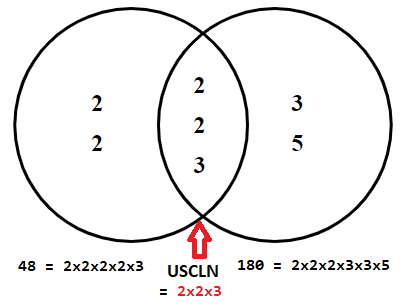
USCLN của 2 số nguyên dương a và b là một số k lớn nhất, sao cho a và b đều chia hết cho k.

BSCNN của 2 số nguyên dương a và b là một số h nhỏ nhất, sao cho h chia hết cho cả a và b.

Lời giải

Một phương pháp đơn giản đề tìm USCLN của a và b là duyệt từ số nhỏ hơn trong 2 số a và b cho đến 1, khi gặp số nào đó mà cả a và b đều chia hết cho nó thì đó chính là USCLN của a và b. Tuy vậy phương pháp này chưa phải là hiệu quả nhất.

Vào thế kỷ 3 TCN, nhà toán học Euclid (phiên âm tiếng Việt là Ơ-clit) đã phát minh ra một giải thuật tìm USCLN của hai số nguyên dương rất hiệu quả được gọi là giải thuật Euclid. Cụ thể về ý tưởng của bài toán, giả sử a lớn hơn b, khi đó việc tính UCSLN của a và b sẽ được đưa về bài toán tính USCLN của a mod b và b vì USCLN(a, b) = USCLN(a mod b, b).

Khi đã tìm được USCLN thì việc tìm BSCNN của hai số nguyên dương a và b khá đơn giản. Khi đó BSCNN(a, b) = (a * b) / UCSLN(a, b).

Tìm USCLN và BSCNN của 2 số a và b trong C++

Ví dụ dưới đây sử dụng giải thuật Euclid để giải quyết bài toán tìm ước số chung lớn nhất (USCLN) và bội số chung nhỏ nhất (BSCNN) của hai số nguyên dương a và b.

/**
 * Chuong trinh tim uoc chung lon nhat (USCLN)
 * va boi so chung nho nhat (BSCNN) cua 2 so a và b
 * 
 * @author viettuts.vn
 */
 
#include <iostream>
 
using namespace std;

/**
 * Tim uoc so chung lon nhat (USCLN)
 */
int USCLN(int a, int b) {
    if (b == 0) return a;
    return USCLN(b, a % b);
}

/**
 * Tim boi so chung nho nhat (BSCNN)
 */
int BSCNN(int a, int b) {
    return (a * b) / USCLN(a, b);
}

/**
 * Ham main
 */
int main() {
 int a, b;
    cout << "Nhap so nguyen duong a = ";
    cin >> a;
    cout << "Nhap so nguyen duong b = ";
    cin >> b;
    // tinh USCLN cua a và b
    printf("USCLN cua %d va %d la: %d, ", a, b, USCLN(a, b));
    // tinh BSCNN cua a và b
    printf("BSCNN cua %d va %d la: %d", a, b, BSCNN(a, b));
}

Kết quả:

Nhap so nguyen duong a = 4
Nhap so nguyen duong b = 6
USCLN cua 4 va 6 la: 2, BSCNN cua 4 va 6 la: 12